Hey, y'all. Just got done with the Edgerton Center Engineering Design workshop, where I mentored high school students on engineering principles. Check out the site at http://edw.scripts.mit.edu. Anyways, one of the projects during the program was a window opener, and their prototype used the standard motor used in the First Robotics Challenge, also known as the CIM motor.

Now, this motor has quite the amount of torque for its small size, designed to run at a maximum of 337 watts at 12 volts, plus, it costs less than $30—quite affordable for EVs. I also figured that the output power could easily be increased by raising the output voltage.
However, this motor has its drawbacks. Looking at the datasheet, one can see that at peak output power (at 12 volts), the efficiency is 41%, meaning more than half the power supplied to the motor is being dissipated as heat. To put that in perspective, the heat wasted in the motor is enough to heat half of my dorm room in the fall (which is quite a large room, by the way)! That much heat would destroy the motor in no time, so I needed a way to determine whether or not it would be feasible tossing this in an EV (in which I would probably put the motors in parallel), without wasting a serious amount of power. I needed to be able to estimate the efficiency.

Here's where MATLAB comes in, I could probably estimate the efficiency by hand, as several websites tell how to calculate peak efficiency in a motor as given at ~10% of rated power [citation needed]. However, I'm still learning about motors and power electronics, and I figured trying to calculate it given the motor parameters, not necessarily from generally used values should be a good learning experience.
First, we need to know what makes a motor inefficient. The main two causes of losses are conduction (resistive) losses, and core (hysteresis) losses.
Conduction losses come from the fact that all motors have some resistance in their coils, and as a result, some of the electric power flowing through the windings is dissipated as heat, which is known as joule heating. That power varies with the square of output torque, because current is directly proportional to torque, because the voltage drop in a resistor is current times resistance (ohms law), and because electrical power is voltage*current.
$\mathrm{P} = \left(\frac{\tau}{k}\right)^2*\mathrm{R}$
(k is the motor constant)
Core losses are a bit more complex. They come from the fact that magnets (electromagnets included) do not lose their all of their magnetic properties when there's no magnet field applied, but require a reverse magnet field to bring them back (this is how permanent magnets work).
The same happens in our motor, and you need extra energy to reverse the magnetic field to turn the motor. The energy required scales with frequency, and because at higher speeds, you have higher reversals, this power varies with the square of rotational velocity.
$\mathrm{P} = \omega^2*h$
(h is a constant relating to the core loss, $\omega$ is rotational velocity).
With that out of the way, we create our model.
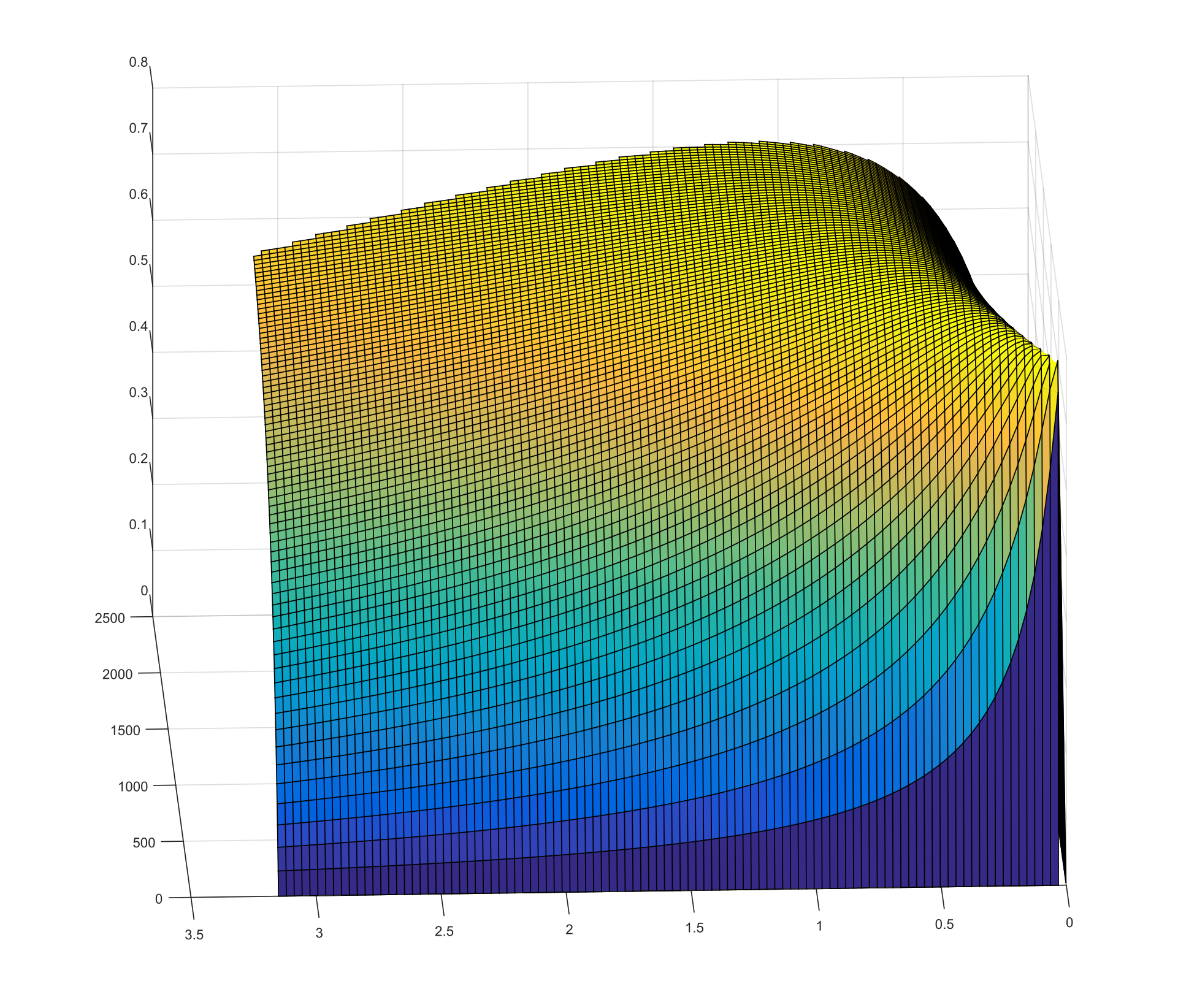
This model takes in parameters, (max current, max voltage, motor constant, motor resistance, hysteresis loss coefficient), and generates power values for the possible torque and speed values. It then adds the conduction and core loss to determine the electrical power required to drive the motor at that point. It then calculates the efficiency with
$\eta = \frac{\mathrm{mechanical power}}{\mathrm{electrical power}}$.
It turns out, that at 48 volts, the maximum efficiency of a CIM motor is 78%, at 2.28 kW, with a torque of 1.323 Nm, and angular velocity of 1572 RPM. It's not great, but much better than the 65% at 12v.

